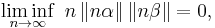Littlewood conjecture

In mathematics, the Littlewood conjecture is an open problem (as of 2011) in Diophantine approximation, posed by John Edensor Littlewood around 1930. It states that for any two real numbers α and β,

\liminf_{n\to\infty} \ n\,\Vert n\alpha\Vert \,\Vert n\beta\Vert = 0,

where \Vert \,\Vert is here the distance to the nearest integer.

Contents

Formulation and explanation

This means the following: take a point (α,β) in the plane, and then consider the sequence of points

(2α,2β), (3α,3β), ... .

For each of these consider the closest lattice point, as determined by multiplying the distance to the closest line with integer x-coordinate by the distance to the closest line with integer y-coordinate. This product will certainly be at most 1/4. The conjecture makes no statement about whether this sequence of values will converge; it typically does not, in fact. The conjecture states something about the limit inferior, and says that there is a subsequence for which the distances decay faster than the reciprocal, i.e.

o(1/n)

in the little-o notation.

Connection to further conjectures

It is known that this would follow from a result in the geometry of numbers, about the minimum on a non-zero lattice point of a product of three linear forms in three real variables: the implication was shown in 1955 by J. W. S. Cassels and Swinnerton-Dyer.[1] This can be formulated another way, in group-theoretic terms. There is now another conjecture, expected to hold for n ≥ 3: it is stated in terms of G = SLn(R), Γ = SLn(Z), and the subgroup D of G of diagonal matrices.

Conjecture: for any g in G/Γ such that Dg is relatively compact (in G/Γ), then Dg is closed.

This in turn is a special case of a general conjecture of Margulis on Lie groups.

Partial results

Progress has been made in showing that the exceptional set of real pairs (α,β) violating the statement of the conjecture must be small. Manfred Einsiedler, Anatole Katok and Elon Lindenstrauss have shown[2] that it must have Hausdorff dimension zero; and in fact is a union of countably many compact sets of box-counting dimension zero. The result was proved by using measure classification theorem for diagonalizable actions of higher-rank groups, and an isolation theorem proved by Lindenstrauss and Barak Weiss.

See also

References

  1. ^ J.W.S. Cassels, H.P.F. Swinnerton-Dyer (1955-06-23). "On the product of three homogeneous linear forms and the indefinite ternary quadratic forms". Philosophical Transactions of the Royal Society of London A 248 (940): 73–96. doi:10.1098/rsta.1955.0010. JSTOR 91633. MR70653. Zbl 0065.27905. 
  2. ^ M. Einsiedler, A. Katok, E. Lindenstrauss (2006-09-01). "Invariant measures and the set of exceptions to Littlewood's conjecture". Annals of Mathematics 164 (2): 513–560. arXiv:math.DS/0612721. doi:10.4007/annals.2006.164.513. MR2247967. Zbl 1109.22004. 

Further reading